|
|
|
|
| |
¿Para qué sirve la aritmética binaria?
|
| |
Todas las operaciones matemáticas (sumas, restas, divisiones, etc.) que realiza la computadora están basadas en la aritmética binaria.
Suma Binaria
|
| |
| La aritmética binaria es muy similar a la aritmética decimal. Por ejemplo, para realizar una suma binaria hay que tener en cuenta la siguiente tabla: |
| |
 |
| |
| Ejemplo 1: Para sumar los números binarios 100102 y 1102 se puede escribir: |
| |
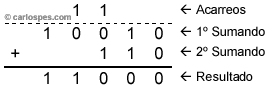 |
| |
Para comprobar si la suma es correcta, podemos convertir los números binarios a base 10. Así pues, aplicando el Teorema Fundamental de la Numeración (TFN) obtendremos:
1º Sumando → 100102 = 1∙24 + 0∙23 + 0∙22 + 1∙21 + 0∙20 = 16 + 0 + 0 + 2 + 0 = 1810
2º Sumando → 1102 = 1∙22 + 1∙21 + 0∙20 = 4 + 2 + 0 = 610
Resultado → 110002 = 1∙24 + 1∙23 + 0∙22 + 0∙21 + 0∙20 = 16 + 8 + 0 + 0 + 0 = 2410
y, efectivamente,
1810 + 610 = 2410 |
| |
| |
| |
Resta Binaria
|
| |
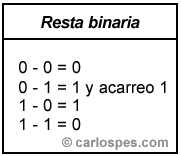
| Si se quiere realizar una resta binaria se debe considerar la siguiente tabla: |
| |
 |
| |
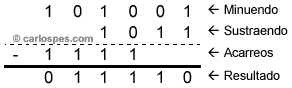
| Ejemplo 2: Para restar los números binarios 1010012 y 10112 escribiremos: |
| |
 |
| |
| |
| |
Multiplicación Binaria
|
| |
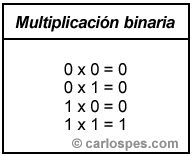
| Para efectuar una multiplicación binaria se tiene que tener en cuenta la siguiente tabla: |
| |
 |
| |
| Ejemplo 3: Para realizar el producto de los números binarios 101012 y 1012 hay que realizar los siguientes cálculos: |
| |
 |
| |
| |
| |
División Binaria
|
| |
| En cuanto a las divisiones binarias, las reglas también son las mismas que en el Sistema Decimal, con la ventaja de que en binario sólo se usan dos dígitos. |
| |
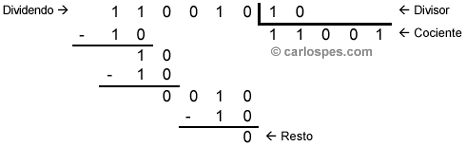
| Ejemplo 4: Para dividir 1100102 entre 102 los cálculos son: |
| |
 |
|
|
|
|
|
|
|
| |
¡Hoy había/n 1 visitantes (1 clics a subpáginas) en ésta página! |
|
|
|
|
|
|
|